rpact and RPACT Cloud in Practical Use

Daniel Sabanés Bové

RPACT

November 20, 2025

rpact and RPACT Cloud in Practical Use

Example illustrating the package concept

Usage inspired by the typical workflow in trial design and conduct:

  • Everything is starting with a design, e.g.:
    design <- getDesignGroupSequential()
  • Find the optimal design parameters:
    R / rpact / RPACT Cloud
  • Calculate the required sample size and power, e.g.:
    getSampleSizeMeans(), getPowerMeans()
  • Optionally perform simulations to confirm the operating characteristics, e.g.:
    getSimulationMeans()
  • Collect your data, import it into R and create an rpact dataset:
    data <- getDataset()
  • Analyze your data: getAnalysisResults(design, data)

Example: Planning and Conducting a Clinical Study Using R and rpact

  • In this fictive example, we will illustrate the planning and conduct of a clinical trial to assess the effectiveness of a new antihypertensive therapy.
  • Each step will be demonstrated using R, primarily with the rpact package and RPACT Cloud.
  • Additional R packages may be used as needed.

Study Design

Objective: To evaluate the efficacy of a new antihypertensive therapy
(compared to a placebo) in patients with hypertension.

Endpoints and Assumptions:

  • Endpoint: Continuous endpoint (blood pressure reduction).
  • Comparison Groups: New Treatment vs. Placebo.
  • Statistical Parameters:
    • One-sided test with \(\alpha\) = 0.025.
    • Power = 80%.

Initial Assumptions and Parameter Estimation

Assumptions:

  • Patients in this study suffer from high blood pressure (grade 2 hypertension), often around 150 mmHg (systolic).
  • The objective is to significantly reduce blood pressure in the treatment group, while no substantial reduction is expected in the placebo group.

Expected Values:

  • Target difference in systolic blood pressure change from baseline:
    12 mmHg (difference in mean reduction between treatment and placebo).
  • Variability of change from baseline:
    Standard deviation of 15 mmHg.

Step 1: Sample Size Calculation

Using rpact we will calculate the required sample size to achieve a power of 80% for detecting a 12 mmHg difference in systolic blood pressure change from baseline in the treatment group relative to the placebo group, assuming a standard deviation of 15 mmHg.

We will see a nice feature when using rpact output in RMarkdown or Quarto docs: you directly get a nicely formatted result output.

Step 1: Sample Size Calculation (cont’d)

# Load the rpact package
library(rpact)

# Define the design parameters for sample size calculation
design <- getDesignGroupSequential(
    kMax = 1, # Only one analysis (classic fixed design)
    alpha = 0.025, # Significance level
    beta = 0.20, # 80% power
    sided = 1 # One-sided test
)

# Estimate sample size
sampleSizeResult <- design |>
    getSampleSizeMeans(
        groups = 2, # Two groups: Treatment vs. Placebo
        alternative = 12, # Expected effect size
        stDev = 15 # Common standard deviation
    )

Step 1: Sample Size Calculation (cont’d)

# Print the summary of the results
sampleSizeResult |> summary()

Sample size calculation for a continuous endpoint

Fixed sample analysis, one-sided significance level 2.5%, power 80%. The results were calculated for a two-sample t-test, H0: mu(1) - mu(2) = 0, H1: effect = 12, standard deviation = 15.

Stage Fixed
Stage level (one-sided) 0.0250
Efficacy boundary (z-value scale) 1.960
Efficacy boundary (t) 8.438
Number of subjects 51.0

Legend:

  • (t): treatment effect scale

Step 1: Sample Size Calculation (cont’d)

Using fetch() we can extract specific quantities from the result object.

# Fetch the number of subjects required
sampleSizeResult |> fetch("Number of subjects fixed")
  nFixed 
51.04927

Step 2: Calculating Power

Now let’s go the other way around - calculate the power for given sample size, and vary other parameters. This helps us to:

  1. Verify the Assumptions: Confirm that the chosen sample size yields the expected 80% power.
  2. Explore Outcome Variability: Observing power across different situations can reveal potential inconsistencies in achieving the target power, especially with variations in standard deviation or effect size.
  3. Adjust Study Design: If the results show that power is consistently below the target, we might need to increase the sample size or reconsider assumptions.

Step 2: Calculating Power (cont’d)

Using the rpact package, we can calculate the power of the study under the defined parameters. Here’s how:

# Define parameters based on initial assumptions
calculatedSampleSize <- ceiling(sampleSizeResult$numberOfSubjects)

powerResult <- design |>
    getPowerMeans(
        groups = 2, # Two groups: Treatment and Placebo
        alternative = 12, # Expected effect size
        stDev = 15, # Common standard deviation
        maxNumberOfSubjects = calculatedSampleSize
    )

Step 2: Calculating Power (cont’d)

Power calculation for a continuous endpoint

Fixed sample analysis, one-sided significance level 2.5%. The results were calculated for a two-sample t-test, H0: mu(1) - mu(2) = 0, power directed towards larger values, H1: effect = 12, standard deviation = 15, number of subjects = 52.

Stage Fixed
Stage level (one-sided) 0.0250
Efficacy boundary (z-value scale) 1.960
Efficacy boundary (t) 8.356
Power 0.8075
Number of subjects 52.0

Legend:

  • (t): treatment effect scale

Step 2: Calculating Power (cont’d)

  • The results show that in 80.75% of the trials the test successfully detects a true difference between treatment and control group regarding change from baseline.
  • Next steps: proceed with further setup and explore possible adjustments based on the outcomes.

Exploring Possible Adjustments Based on Power Calculation Outcomes

  1. Varying Effect Size: If the expected effect size of 12 mmHg is optimistic, we could calculate a scenario with a smaller effect size (e.g., 10 mmHg) to see how it affects the required sample size and power.
  2. Varying Standard Deviation: The assumed standard deviation of 15 mmHg might vary across patient groups. Increasing it to 16 or 17 mmHg would allow us to explore how higher variability impacts power and the required sample size.

Possible Adjustments

Here’s R code to analyze the scenarios described above:

# Define scenarios for adjustments
scenarios <- list(
    list(alternative = 10, stDev = 15), # 1: Reduced effect
    list(alternative = 10, stDev = 14), # 2: Reduced effect + sd
    list(alternative = 11, stDev = 15), # 3: Reduced effect
    list(alternative = 11, stDev = 14), # 4: Reduced effect + sd
    list(alternative = 12, stDev = 15), # 5: Base scenario
    list(alternative = 13, stDev = 16), # 6: Incr. sd + effect
    list(alternative = 13, stDev = 17), # 7: Incr. sd + effect
    list(alternative = 12, stDev = 16), # 8: Increased sd
    list(alternative = 12, stDev = 17) # 9: Increased sd
)

# Run calculations for each scenario
results <- scenarios |>
    lapply(function(scenario) {
        getPowerMeans(
            design = design,
            groups = 2,
            alternative = scenario$alternative,
            stDev = scenario$stDev,
            maxNumberOfSubjects = 52
        )
    })

# Fetch only the power from the result objects
x <- sapply(results, function(result) {
    result |> fetch("Overall reject")
})

Possible Adjustments (cont’d)

# Display results for each scenario
scenarios |>
    bind_rows() |>
    mutate(power = x) |>
    as.data.frame() |>
    set_rownames(paste("Scenario", 1:length(x))) |>
    kable()
alternative stDev power
Scenario 1 10 15 0.6544534
Scenario 2 10 14 0.7142007
Scenario 3 11 15 0.7366421
Scenario 4 11 14 0.7933714
Scenario 5 12 15 0.8074858
Scenario 6 13 16 0.8193392
Scenario 7 13 17 0.7715373
Scenario 8 12 16 0.7555122
Scenario 9 12 17 0.7040188

Possible Adjustments (cont’d)

Interpreting the results from the different scenarios:

  1. Base scenario (52 subjects, 12 mmHg effect, 15 mmHg SD): Verifying the original power (around 80.75%).
  2. Reduced effect size (10 mmHg effect): With a smaller effect size, the power drops to 65.45%.
  3. Increased standard deviation (17 mmHg SD): Increasing variability lowers the power to 70.4%, as greater variability results in less precise outcomes.

By exploring these adjustments, we gain insight into whether a larger sample or refined target parameters might be needed for a more reliable assessment of the new treatments’s efficacy.

Exploring Scenarios with Larger Treatment Group

  • Explore scenarios with unequal allocation ratios, assigning more participants to the treatment group than to the control group.
  • This approach allows more patients the potential benefit of the new therapy while still maintaining a control group for reliable statistical comparison.
  • The allocationRatioPlanned argument in rpact enables us to specify these ratios.

Scenario Adjustments Using Unequal Allocation Ratios

Here are the new scenarios we will examine:

  1. Base scenario (1:1 allocation): Both groups (treatment and control) have equal numbers of participants.
  2. 2:1 allocation: For every 1 participant in the control group, 2 are assigned to the treatment group.
  3. 3:1 allocation: For every 1 participant in the control group, 3 are assigned to the treatment group.

Comparing Different Allocation Ratios

Using the rpact package, we can set up and calculate these scenarios with the allocationRatioPlanned parameter:

# Define the initial design
design <- getDesignGroupSequential(
    kMax = 1,
    alpha = 0.025,
    beta = 0.2,
    sided = 1
)

# Define scenarios for different allocation ratios
scenarios <- list(
    list(allocationRatio = 1), # 1:1 allocation
    list(allocationRatio = 2), # 2:1 allocation
    list(allocationRatio = 3) # 3:1 allocation
)

# Run calculations for each scenario with specified allocation ratios
results <- scenarios |>
    lapply(function(scenario) {
        getPowerMeans(
            design = design,
            groups = 2,
            alternative = 12,
            stDev = 15,
            maxNumberOfSubjects = 50,
            allocationRatioPlanned = scenario$allocationRatio
        )
    })

# Fetch only the power from the result objects
x <- sapply(results, function(result) {
    result |> fetch("Overall reject")
})

Comparing Different Allocation Ratios (cont’d)

# Display results for each scenario
scenarios |>
    bind_rows() |>
    mutate(power = x) |>
    as.data.frame() |>
    set_rownames(paste("Scenario", 1:length(x))) |>
    kable()
allocationRatio power
Scenario 1 1 0.7914502
Scenario 2 2 0.7431284
Scenario 3 3 0.6701351

Let’s assume that a 2:1 allocation shall be used going forward.

Continuing with a Group-Sequential Design to Open Up the Opportunity for Early Stopping

Given the slight reduction in power observed with the 2:1 allocation ratio (Power = 74.3%), we can implement a group-sequential design with an interim analysis instead of simply increasing the sample size.

  • Planned Interim Analysis:
    • After enrolling a number yet to be determined participants, an interim analysis will be conducted.
  • Possible Outcomes:
    • If the treatment shows significant efficacy at the interim point, the study can be stopped early to avoid additional recruitment.
    • If efficacy is not yet demonstrated, we proceed to the full planned sample size.

Step 1: Calculate the sample size for a fixed design

First we start again with a fixed sample size design:

numberOfSubjectsFixed <- getDesignGroupSequential(
    kMax = 1,
    alpha = 0.025,
    beta = 0.2,
    sided = 1
) |>
    getSampleSizeMeans(
        groups = 2,
        alternative = 12,
        stDev = 15,
        allocationRatioPlanned = 2
    ) |>
    fetch("Number of subjects fixed") |>
    ceiling()
numberOfSubjectsFixed
nFixed 
    58

We need numberOfSubjectsFixed for the subsequent power analysis.

Step 2: Define the Group-Sequential Design with an Interim Analysis

  • We’ll use rpact to define a group-sequential design with two planned analyses.
  • The first analysis will occur after enrolling n subjects, with a final analysis if the study proceeds to the full sample.
  • n shall be determined by exploring different information rates

Design Comparison with RPACT Cloud

Design Comparison in R

Here’s how to set up the design comparison in R:

First we define the possible information rates at which to conduct the interim analysis.

# Define scenarios
scenarios <- list(
    list(informationRate = 0.5),
    list(informationRate = 0.6),
    list(informationRate = 0.7),
    list(informationRate = 0.8),
    list(informationRate = 0.9)
)

Design Comparison in R (cont’d)

# Run calculations for each scenario
results <- scenarios |>
    lapply(function(scenario) {
        getDesignGroupSequential(
            informationRates = c(scenario$informationRate, 1),
            alpha = 0.025,
            sided = 1,
            typeOfDesign = "OF"
        ) |>
            getPowerMeans(
                groups = 2,
                alternative = 12,
                stDev = 15,
                maxNumberOfSubjects = numberOfSubjectsFixed, # 58
                allocationRatioPlanned = 2
            )
    })

Design Comparison in R (cont’d)

# Display results for each scenario
x <- lapply(results, function(result) {
    result |> fetch("Expected number of subjects", "Early stop")
}) |>
    bind_rows()

#| echo: true
scenarios |>
    bind_rows() |>
    cbind(x) |>
    as.data.frame() |>
    set_rownames(paste("Scenario", 1:length(scenarios))) |>
    kable()
informationRate expectedNumberOfSubjects earlyStop
Scenario 1 0.5 51.86201 0.2116549
Scenario 2 0.6 49.88180 0.3499223
Scenario 3 0.7 49.56749 0.4846273
Scenario 4 0.8 50.99013 0.6042989
Scenario 5 0.9 53.90422 0.7061693

In this example we decide to use information rate 0.7 because the expected number of subjects is lowest and the probability for an early stopping is nearly 50%.

Sample Size with an Interim Analysis

design <- getDesignGroupSequential(
    informationRates = c(0.7, 1),
    alpha = 0.025, # Overall significance level
    beta = 0.2, # Power 80%
    sided = 1, # One-sided test
    typeOfDesign = "OF" # O'Brien & Fleming design
)

sampleSizeResult <- getSampleSizeMeans(
    design = design,
    groups = 2,
    alternative = 12, # Target effect
    stDev = 15, # Common standard deviation
    allocationRatioPlanned = 2 # 2:1 allocation
)

# Print the summary of the results
sampleSizeResult |>
    summary()

Sample size calculation for a continuous endpoint

Sequential analysis with a maximum of 2 looks (group sequential design), one-sided overall significance level 2.5%, power 80%. The results were calculated for a two-sample t-test, H0: mu(1) - mu(2) = 0, H1: effect = 12, standard deviation = 15, planned allocation ratio = 2.

Stage 1 2
Planned information rate 70% 100%
Cumulative alpha spent 0.0082 0.0250
Stage levels (one-sided) 0.0082 0.0223
Efficacy boundary (z-value scale) 2.400 2.008
Efficacy boundary (t) 12.508 8.566
Cumulative power 0.4861 0.8000
Number of subjects 40.7 58.2
Expected number of subjects under H1 49.7
Exit probability for efficacy (under H0) 0.0082
Exit probability for efficacy (under H1) 0.4861

Legend:

  • (t): treatment effect scale

Sample Size with an Interim Analysis (cont’d)

sampleSizeResult |>
    fetch(
        "Expected number of subjects under H1",
        "Early stop"
    )
$expectedNumberOfSubjectsH1
[1] 49.72055

$earlyStop
[1] 0.486071

Step 3: Calculate the Power of the Group-Sequential Design

To confirm that the design meets the target power while allowing for early stopping, we calculate the power of the study under the adjusted parameters:

powerResult <- getPowerMeans(
    design = design,
    groups = 2,
    alternative = 12, # Expected effect size
    stDev = 15, # Common standard deviation
    # Sample size per stage from previous calculation
    maxNumberOfSubjects = ceiling(sampleSizeResult$numberOfSubjects)[2, 1],
    allocationRatioPlanned = 2 # Allocation ratio 2:1
)

# Print the summary of the results
powerResult |>
    summary()

Power calculation for a continuous endpoint

Sequential analysis with a maximum of 2 looks (group sequential design), one-sided overall significance level 2.5%. The results were calculated for a two-sample t-test, H0: mu(1) - mu(2) = 0, power directed towards larger values, H1: effect = 12, standard deviation = 15, maximum number of subjects = 59, planned allocation ratio = 2.

Stage 1 2
Planned information rate 70% 100%
Cumulative alpha spent 0.0082 0.0250
Stage levels (one-sided) 0.0082 0.0223
Efficacy boundary (z-value scale) 2.400 2.008
Efficacy boundary (t) 12.416 8.506
Cumulative power 0.4930 0.8057
Number of subjects 41.3 59.0
Expected number of subjects under H1 50.3
Exit probability for efficacy (under H0) 0.0082
Exit probability for efficacy (under H1) 0.4930

Legend:

  • (t): treatment effect scale

Adding a Futility Analysis

  • Now we want to find a futility bound for the interim analysis that depends on a clinical relevant threshold.
  • We assume that it makes no sense to continue the analysis when the observed treatment effect is 5 mmHg or less
  • The minimum futility bound must be 0 because otherwise the effect would go in the wrong direction
  • Ultimately, we go for a boundary of 2 mmHg on treatment effect scale
# Define scenarios
scenarios <- list(
    list(futilityBounds = -1),
    list(futilityBounds = -0.5),
    list(futilityBounds = 0),
    list(futilityBounds = 0.5),
    list(futilityBounds = 1),
    list(futilityBounds = 1.5)
)

Adding a Futility Analysis (cont’d)

# Run calculations for each scenario
results <- scenarios |>
    lapply(function(scenario) {
        getDesignGroupSequential(
            informationRates = c(0.7, 1),
            futilityBounds = scenario$futilityBounds,
            alpha = 0.025,
            sided = 1,
            typeOfDesign = "OF"
        ) |>
            getSampleSizeMeans(
                groups = 2,
                alternative = 12,
                stDev = 15,
                allocationRatioPlanned = 2
            )
    })

Adding a Futility Analysis (cont’d)

# Display results for each scenario
x <- sapply(results, function(result) {
    result |> fetch("Futility bounds (treatment effect scale)")
})

#| echo: true
scenarios |>
    bind_rows() |>
    mutate("Futility bounds (treatment effect scale)" = x) |>
    as.data.frame() |>
    set_rownames(paste("Scenario", 1:length(x))) |>
    kable()
futilityBounds Futility bounds (treatment effect scale)
Scenario 1 -1.0 -5.050045
Scenario 2 -0.5 -2.512664
Scenario 3 0.0 0
Scenario 4 0.5 2.508815
Scenario 5 1.0 4.97699
Scenario 6 1.5 7.102175

Find Futility Bound on the Z Scale

We will first search the futility bound on the Z scale that corresponds to a treatment effect of 2 mmHg. We do this with stats::uniroot():

?uniroot

One Dimensional Root (Zero) Finding

Description

The function uniroot searches the interval from lower to upper for a root (i.e., zero) of the function f with respect to its first argument.

uniroot(
    f,
    interval,
    ...,
    lower = min(interval),
    upper = max(interval),
    f.lower = f(lower, ...),
    f.upper = f(upper, ...),
    extendInt = c("no", "yes", "downX", "upX"),
    check.conv = FALSE,
    tol = .Machine$double.eps^0.25,
    maxiter = 1000,
    trace = 0
)

Find Futility Bound on the Z Scale (cont’d)

soughtBoundaryTreatmentEffectScale <- 2
futilityBound <- uniroot(
    function(x) {
        soughtBoundaryTreatmentEffectScale -
            getDesignGroupSequential(
                informationRates = c(0.7, 1),
                futilityBounds = x,
                alpha = 0.025,
                sided = 1,
                typeOfDesign = "OF"
            ) |>
            getSampleSizeMeans(
                groups = 2,
                alternative = 12,
                stDev = 15,
                allocationRatioPlanned = 2
            ) |>
            fetch("Futility bounds (treatment effect scale)") |>
            as.numeric()
    },
    lower = 0,
    upper = 2
)$root
futilityBound
[1] 0.3985836

Find Futility Bound on the Z Scale (cont’d)

Alternatively, we can also calculate this in an approximate closed form here via:

\[ u_{1}^{0} = \delta_{0} \sqrt{\frac{n_{11}n_{21}}{n_{11} + n_{21}}} / \sigma \]

n1 <- sampleSizeResult$numberOfSubjects[2, 1]
n11 <- n1 * 2 / 3
n21 <- n1 * 1 / 3

futilityBoundClosed <- soughtBoundaryTreatmentEffectScale * sqrt(0.7 * n11 * n21 / (n11 + n21)) / 15
futilityBoundClosed
[1] 0.4012131

Sample Size with Futility Bound

sampleSizeResult <- getDesignGroupSequential(
    informationRates = c(0.7, 1),
    futilityBounds = futilityBoundClosed,
    alpha = 0.025,
    sided = 1,
    typeOfDesign = "OF"
) |>
    getSampleSizeMeans(
        groups = 2,
        alternative = 12,
        stDev = 15,
        allocationRatioPlanned = 2
    )

Sample Size with Futility Bound (cont’d)

sampleSizeResult |> summary()

Sample size calculation for a continuous endpoint

Sequential analysis with a maximum of 2 looks (group sequential design), one-sided overall significance level 2.5%, power 80%. The results were calculated for a two-sample t-test, H0: mu(1) - mu(2) = 0, H1: effect = 12, standard deviation = 15, planned allocation ratio = 2.

Stage 1 2
Planned information rate 70% 100%
Cumulative alpha spent 0.0082 0.0250
Stage levels (one-sided) 0.0082 0.0223
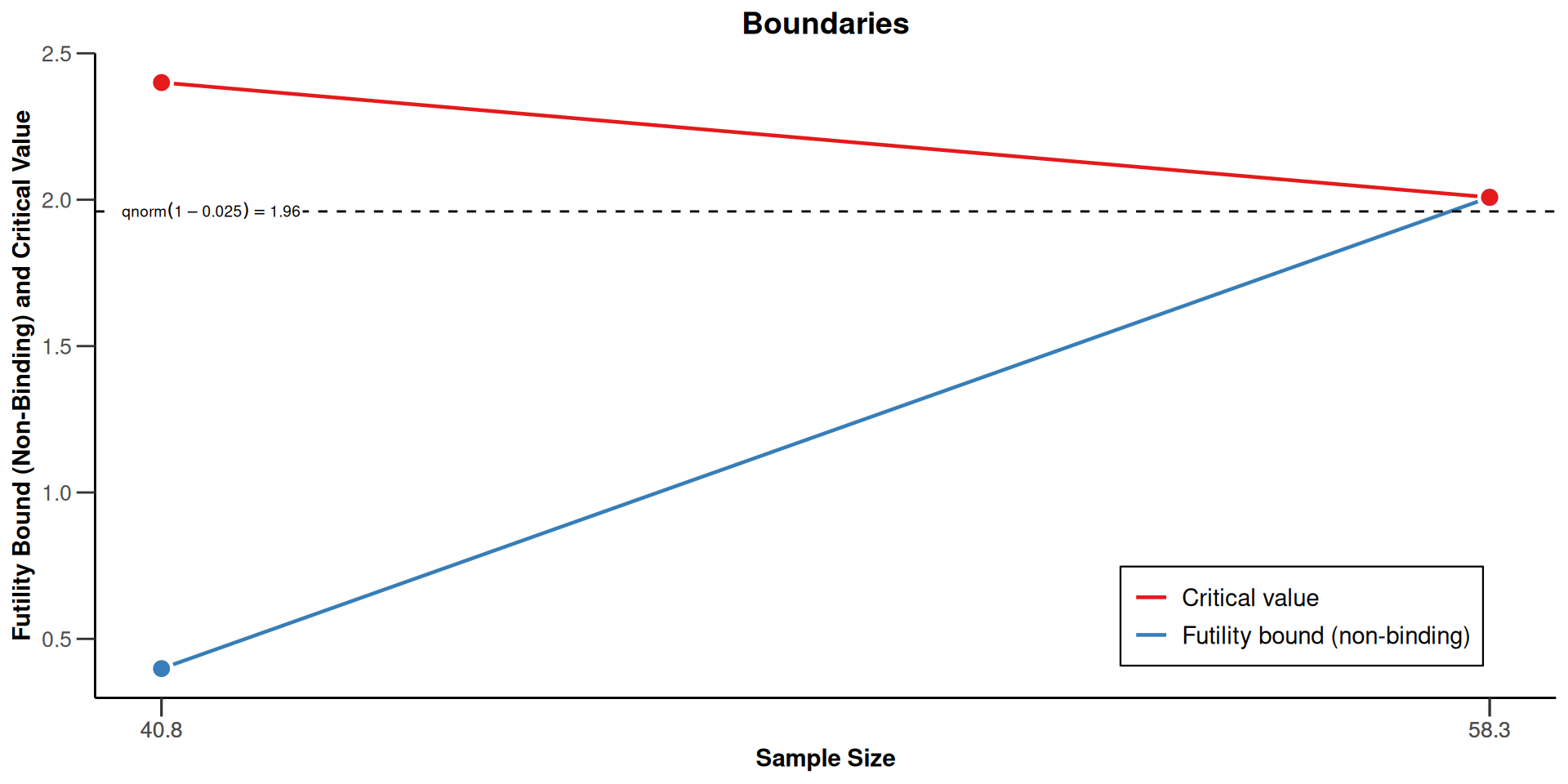
Efficacy boundary (z-value scale) 2.400 2.008
Futility boundary (z-value scale) 0.401
Efficacy boundary (t) 12.496 8.558
Futility boundary (t) 2.013
Cumulative power 0.4869 0.8000
Number of subjects 40.8 58.3
Expected number of subjects under H1 49.4
Overall exit probability (under H0) 0.6641
Overall exit probability (under H1) 0.5116
Exit probability for efficacy (under H0) 0.0082
Exit probability for efficacy (under H1) 0.4869
Exit probability for futility (under H0) 0.6559
Exit probability for futility (under H1) 0.0246

Legend:

  • (t): treatment effect scale

Plot the Design with Futility Bound

# nMax <- ceiling(sampleSizeResult$numberOfSubjects)[2,1]
getDesignGroupSequential(
    informationRates = c(0.7, 1),
    futilityBounds = futilityBound,
    alpha = 0.025,
    sided = 1,
    typeOfDesign = "OF"
) |>
    plot(type = 1, nMax = 60)

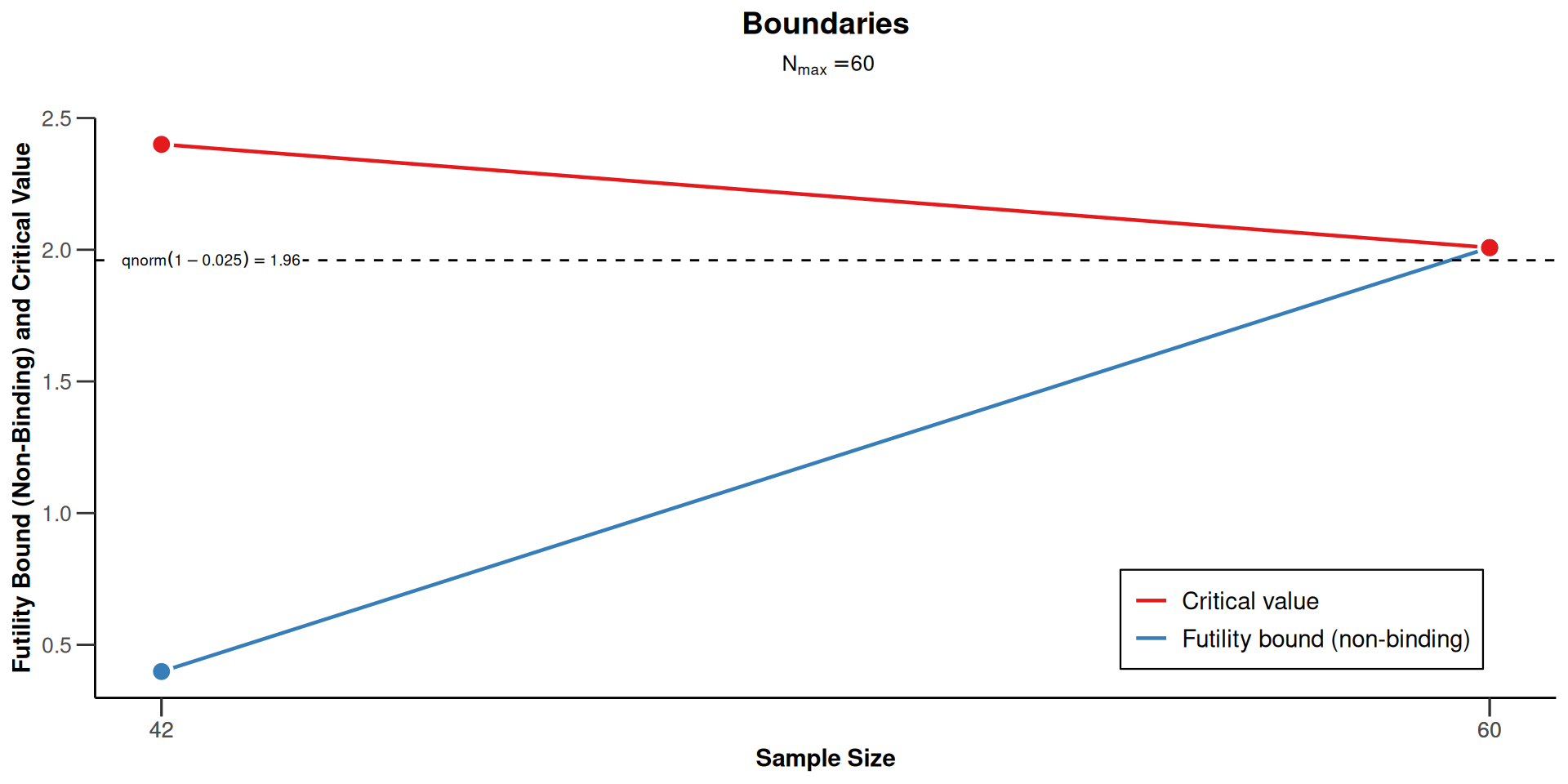
Plot the Design with Futility Bound (cont’d)

getDesignGroupSequential(
    informationRates = c(0.7, 1),
    futilityBounds = futilityBound,
    alpha = 0.025,
    sided = 1,
    typeOfDesign = "OF"
) |>
    getSampleSizeMeans(
        groups = 2,
        alternative = 12,
        stDev = 15,
        allocationRatioPlanned = 2
    ) |>
    plot(type = 1)

Plot the Design with Futility Bound (cont’d)

Simulations to Study Operating Characteristics

  • In this example, we could of course skip simulations, because for a continuous outcome with known standard deviation we can calculate everything in closed form.

  • However, to illustrate the simulation capabilities of rpact, we perform a simulation study to confirm the operating characteristics of our group-sequential design with futility stopping.

  • This is important for non-normal endpoints and adaptive designs where closed form solutions are not available.

Simulation Setup

Now we just call getSimulationMeans() with the design and parameters defined above:

simResults <- getDesignGroupSequential(
    informationRates = c(0.7, 1),
    futilityBounds = futilityBound,
    alpha = 0.025,
    sided = 1,
    typeOfDesign = "OF"
) |> 
    getSimulationMeans(
        groups = 2,
        alternative = c(0, 12), # H0 and H1
        stDev = 15,
        allocationRatioPlanned = 2,
        plannedSubjects = c(41, 59),
        maxNumberOfIterations = 1000,
        seed = 12345
    )

Simulation Results (cont’d)

simResults |> summary()

Simulation of a continuous endpoint

Sequential analysis with a maximum of 2 looks (group sequential design), one-sided overall significance level 2.5%. The results were simulated for a two-sample t-test (normal approximation), H0: mu(1) - mu(2) = 0, power directed towards larger values, H1: effect as specified, standard deviation = 15, planned cumulative sample size = c(41, 59), planned allocation ratio = 2, simulation runs = 1000, seed = 12345.

Stage 1 2
Planned information rate 70% 100%
Cumulative alpha spent 0.0082 0.0250
Stage levels (one-sided) 0.0082 0.0223
Efficacy boundary (z-value scale) 2.400 2.008
Futility boundary (z-value scale) 0.399
Cumulative power, alt. = 0 0.0040 0.0210
Cumulative power, alt. = 12 0.5060 0.8120
Stage-wise number of subjects, alt. = 0 41.0 18.0
Stage-wise number of subjects, alt. = 12 41.0 18.0
Expected number of subjects under H1, alt. = 0 47.4
Expected number of subjects under H1, alt. = 12 49.5
Conditional power (achieved), alt. = 0 0.1604
Conditional power (achieved), alt. = 12 0.5304
Exit probability for efficacy, alt. = 0 0.0040
Exit probability for efficacy, alt. = 12 0.5060
Exit probability for futility, alt. = 0 0.6390
Exit probability for futility, alt. = 12 0.0230

Legend:

  • alt.: alternative

Simulation Results (cont’d)

Interpretation:

  • We can see the type I error control:
    Cumulative power, alt. = 0 is 2.1% at the final analysis.
  • We can see the power:
    Cumulative power, alt. = 12 is 81.2% at the final analysis.
  • We can confirm that around half of the trials would already stop successfully at the interim analysis under the alternative hypothesis:
    Exit probability for efficacy, alt. = 12 is 50.6%

Collect and Analyse Data

Download the example dataset: trial_data_stage1.csv

trialDataStage1 <- read.csv(here::here("data/trial_data_stage1.csv"))
trialDataStage1$group <- factor(trialDataStage1$group)
trialDataStage1 |>
    as_tibble()
# A tibble: 42 × 4
   subjectId group bloodPressureBaseline bloodPressure
       <int> <fct>                 <dbl>         <dbl>
 1         1 1                      150.          138.
 2         2 1                      144.          160.
 3         3 1                      151.          128.
 4         4 1                      157.          147.
 5         5 1                      153.          136.
 6         6 1                      155.          146.
 7         7 1                      154.          120.
 8         8 1                      150.          173.
 9         9 1                      149.          147.
10        10 1                      145.          113.
# ℹ 32 more rows

The Dataset

trialData <- trialDataStage1 |>
    mutate(bloodPressureDiff = bloodPressure - bloodPressureBaseline)
trialData |>
    as_tibble()
# A tibble: 42 × 5
   subjectId group bloodPressureBaseline bloodPressure bloodPressureDiff
       <int> <fct>                 <dbl>         <dbl>             <dbl>
 1         1 1                      150.          138.            -11.6 
 2         2 1                      144.          160.             15.8 
 3         3 1                      151.          128.            -23.2 
 4         4 1                      157.          147.             -9.72
 5         5 1                      153.          136.            -17.5 
 6         6 1                      155.          146.             -8.76
 7         7 1                      154.          120.            -34.4 
 8         8 1                      150.          173.             22.9 
 9         9 1                      149.          147.             -2.66
10        10 1                      145.          113.            -31.7 
# ℹ 32 more rows

Data Analysis

rpact requires the summary statistics, therefore let’s calculate them:

dataSummary <- trialData |>
    group_by(group) |>
    summarise(
        n = n(),
        meanBaseline = mean(bloodPressureBaseline),
        stDevBaseline = sd(bloodPressureBaseline),
        meanTherapy = mean(bloodPressure),
        stDevTherapy = sd(bloodPressure),
        mean = mean(bloodPressureDiff),
        stDev = sd(bloodPressureDiff)
    )
dataSummary |>
    kable()
group n meanBaseline stDevBaseline meanTherapy stDevTherapy mean stDev
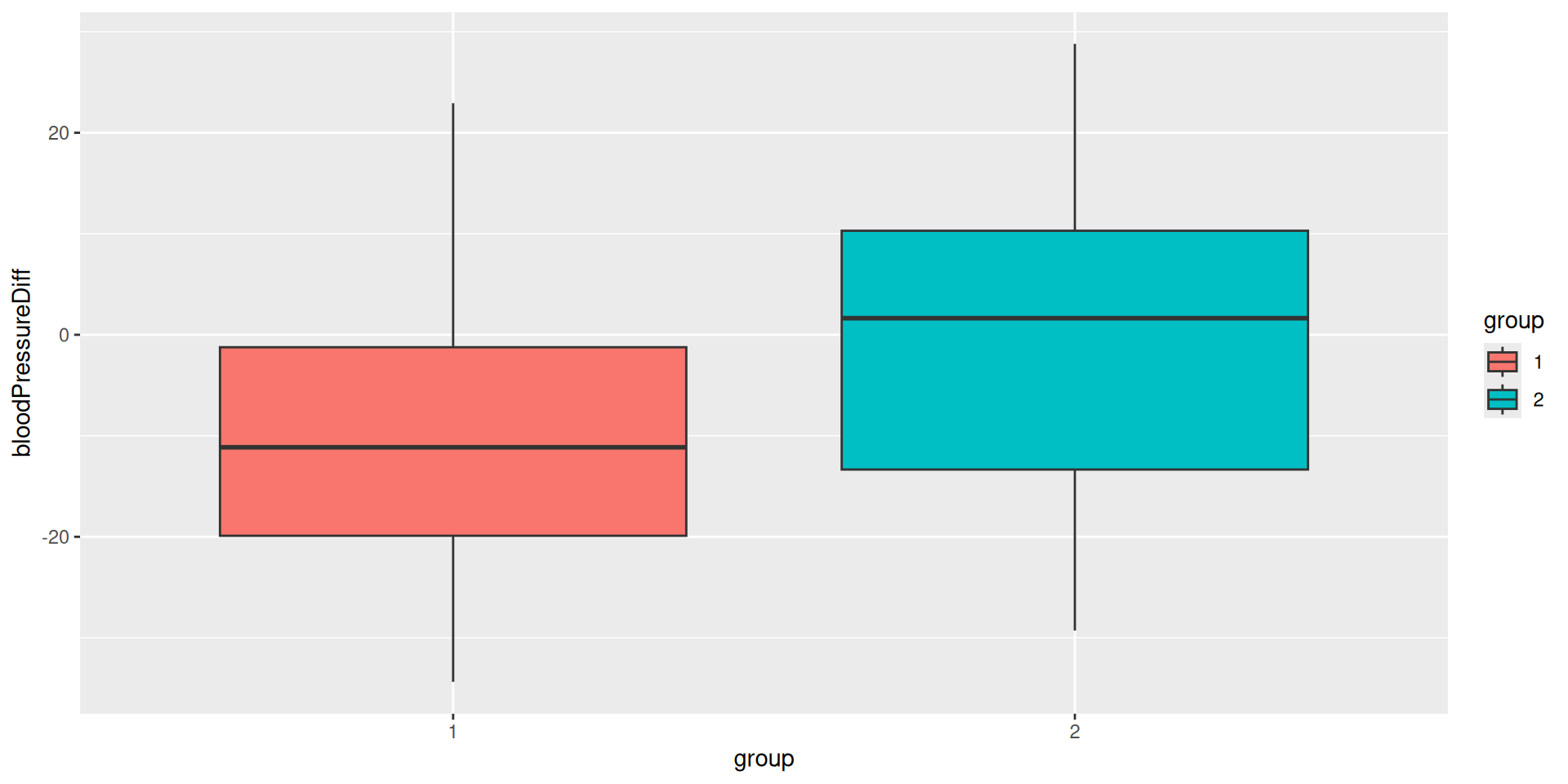
1 28 149.2407 5.677756 139.0127 14.33155 -10.2280732 14.07891
2 14 148.1788 3.743160 147.7018 17.22372 -0.4770206 17.14525

Plot the trial data

library(ggplot2)
ggplot(
    aes(x = group, y = bloodPressureDiff, fill = group),
    data = trialData
) +
    geom_boxplot(na.rm = TRUE)

Create an rpact Dataset

Create an rpact dataset from summary statistics of the trial data:

library(tidyr)
datasetStage1 <- dataSummary |>
    select(group, n, mean, stDev) |>
    mutate(stage = rep(1, nrow(dataSummary))) |>
    pivot_wider(
        names_from = "group",
        values_from = c("n", "mean", "stDev"),
        names_sep = ""
    ) |>
    getDataset()

Interim Analysis: First Look Results

getAnalysisResults(
    design = design,
    dataInput = datasetStage1,
    directionUpper = FALSE,
    nPlanned = 18,
    allocationRatioPlanned = 2,
    stDevH1 = 15
) |>
    summary()

Analysis results for a continuous endpoint

Sequential analysis with 2 looks (group sequential design), one-sided overall significance level 2.5%. The results were calculated using a two-sample t-test, equal variances option. H0: mu(1) - mu(2) = 0 against H1: mu(1) - mu(2) < 0. The conditional power calculation with planned sample size is based on planned allocation ratio = 2, overall effect = -9.751, and assumed standard deviation = 15.

Stage 1 2
Planned information rate 70% 100%
Cumulative alpha spent 0.0082 0.0250
Stage levels (one-sided) 0.0082 0.0223
Efficacy boundary (z-value scale) 2.400 2.008
Cumulative effect size -9.751
Cumulative (pooled) standard deviation 15.144
Overall test statistic -1.967
Overall p-value 0.0281
Test action continue
Conditional rejection probability 0.2271
Planned sample size 18
Conditional power 0.7094
95% repeated confidence interval [-22.171; 2.669]
Repeated p-value 0.0636

Note that we must set directionUpper = FALSE because we have a higher blood pressure reduction in the treatment group, i.e., the blood pressure reduction difference between control and treatment is negative.

Final analysis: Second Look Results

Download the example dataset: trial_data.csv

trialData <- read.csv(here::here("data/trial_data.csv"))
trialData$group <- factor(trialData$group)
trialData |>
    as_tibble()
# A tibble: 60 × 5
   subjectId stage group bloodPressureBaseline bloodPressure
       <int> <int> <fct>                 <dbl>         <dbl>
 1         1     1 1                      150.          138.
 2         2     1 1                      144.          160.
 3         3     1 1                      151.          128.
 4         4     1 1                      157.          147.
 5         5     1 1                      153.          136.
 6         6     1 1                      155.          146.
 7         7     1 1                      154.          120.
 8         8     1 1                      150.          173.
 9         9     1 1                      149.          147.
10        10     1 1                      145.          113.
# ℹ 50 more rows

Alternative Calculation

Alternatively we can use the emmeans package together with a model definition to load the raw data into an rpact dataset.

library(emmeans)
trialData$group <- relevel(trialData$group, ref = "2")
trialData$bloodPressureDiff <-
    trialData$bloodPressure - trialData$bloodPressureBaseline
dataset <- getDataset(
    lm(bloodPressureDiff ~ group, data = trialData, subset = (stage == 1)) |>
        emmeans("group"),
    lm(bloodPressureDiff ~ group, data = trialData, subset = (stage == 2)) |>
        emmeans("group")
)

Note: Here we are not interested in the model output but we need it to compute the estimated marginal means (EMMs; least-squares means) for the factor group in the model. This type of raw data import is particularly useful when the raw data contains covariates that need to be adjusted for.

Alternative Calculation (cont’d)

dataset |> summary()

Dataset of means

The dataset contains the sample sizes, means, and standard deviations of one treatment and one control group. The total number of looks is two; stage-wise and cumulative data are included.

Stage 1 1 2 2
Group 1 2 1 2
Stage-wise sample size 28 14 12 6
Cumulative sample size 28 14 40 20
Stage-wise mean -10.228 -0.477 -13.268 0.313
Cumulative mean -10.228 -0.477 -11.140 -0.240
Stage-wise standard deviation 15.144 15.144 15.275 15.275
Cumulative standard deviation 15.144 15.144 15.052 14.780

Alternative Calculation (cont’d)

Note that the standard deviation looks different depending of the method you use to import the raw data:

  • dplyr: group-wise standard deviations
  • emmeans: pooled standard deviations

For the analysis with rpact this makes no difference.

Alternative Calculation (cont’d)

getAnalysisResults(
    design = design,
    dataInput = dataset,
    directionUpper = FALSE
) |>
    summary()

Analysis results for a continuous endpoint

Sequential analysis with 2 looks (group sequential design), one-sided overall significance level 2.5%. The results were calculated using a two-sample t-test, equal variances option. H0: mu(1) - mu(2) = 0 against H1: mu(1) - mu(2) < 0.

Stage 1 2
Planned information rate 70% 100%
Cumulative alpha spent 0.0082 0.0250
Stage levels (one-sided) 0.0082 0.0223
Efficacy boundary (z-value scale) 2.400 2.008
Cumulative effect size -9.751 -10.900
Cumulative (pooled) standard deviation 15.144 14.964
Overall test statistic -1.967 -2.660
Overall p-value 0.0281 0.0050
Test action continue reject
Conditional rejection probability 0.2271
95% repeated confidence interval [-22.171; 2.669] [-19.311; -2.489]
Repeated p-value 0.0636 0.0054
Final p-value 0.0107
Final confidence interval [-18.228; -1.525]
Median unbiased estimate -10.004

Thank you!

Questions and Answers